이전 포스팅 참조 : 전기력, 쿨롱의 법칙과 중첩의 원리
이전에 우리는 원천 전하와 실험 전하 시이에 작용하는 힘, 전기력을 쿨롱의 법칙과 중첩의 원리를 통해 구해봤습니다. 두 물체 사이에 작용하는 힘을 구하기 위해서는 두 물체가 존재해야만 한다는 점은 아주 당연한 일입니다. 하지만, 만약 하나의 물체가 어떤 분포를 가지고 있는지만 알고 있을 때, 아직 배치하지 않은 실험 전하에 작용하는 힘을 알 수 있다면 어떨까요? 이 생각에서 나온 개념이 바로 '전기장 (Electric Field)'입니다.
전기장 (Electric Field)
이전 포스팅에서 진공에서 어떤 전하 밀도($\rho$)를 가지는 원천 전하와 실험 전하($Q$) 사이에 작용하는 전기력은 다음과 같다는 걸 알아봤습니다. $$ \mathbf{F} = \frac{1}{4\pi\epsilon_0} \int_V \frac{Q\rho(\mathbf{s})}{r'^2} \hat{\mathbf{r}}' d\tau $$

위의 힘에 대한 식에서 실험 전하를 나눈 식을 전기장으로 정의합니다. 다시 말하면, $$ \begin{align} \mathbf{F} & = \frac{1}{4\pi\epsilon_0} \int_V \frac{Q\rho(\mathbf{s})}{r'^2} \hat{\mathbf{r}}' d\tau \\ & = Q \cdot \frac{1}{4\pi\epsilon_0} \int_V \frac{\rho(\mathbf{s})}{r'^2} \hat{\mathbf{r}}' d\tau \\ & = Q \cdot \mathbf{E} \end{align} $$ $$ \therefore \mathbf{E} = \frac{1}{4\pi\epsilon_0} \int_V \frac{\rho(\mathbf{s})}{r'^2} \hat{\mathbf{r}}' d\tau.$$ 수식적으로는 단순히 $\mathbf{F}$에 $Q$를 나눈 것이므로, $\mathbf{E}$는 주어진 원천 전하의 분포가 어떤 위치에서 단위 전하 당 가하는 힘을 나타냅니다.
굳이 왜 전기력이라는 물리량을 두고 왜 전기장을 쓰는 것인가에 대해 생각해봅시다. 전기력은 특정 두 물체 사이에 나타나는 힘을 의미하기 때문에, 이미 힘이 존재하고 있는 상황이고, 전기장은 원천 전하의 분포만 정해져 있는 상황이라서 앞으로 배치될 실험 전하에 작용하는 힘이 어떻게 될 것인지를 예측하는 물리량이라는 차이점이 있습니다.
전기 선속 (Electric Flux)
위 전기장을 이해하는 데에 도움을 주는 방법 중 하나로 전기 선속(Electric Flux)을 통한 방법이 있습니다. 어떤 원천 점전하가 $+q$가 원점에 하나 존재할 때, 이 점전하가 만드는 전기장을 생각해 봅시다. 전기장은 '벡터장(Vector Field)'이기 때문에, 어느 위치 한 점을 잡더라도 그 지점에서의 $+q$가 만드는 전기장을 크기와 방향을 가지는 벡터, 즉, 길이와 방향성을 가지는 화살표로 나타낼 수 있습니다.

혹은 다음과 같이 생각해 볼 수 있습니다. $+q$로부터 생성된 전기장이 '뻗어나가는' 방향으로 화살표를 끊지 않고 그리는 것입니다. 이 경우, 전기장의 방향은 선이 뻗어나가는 방향임은 분명하게 나타낼 수 있으나, 전기장의 세기는 앞의 경우처럼 각 위치마다 벡터를 표시하지 않기 때문에(각 위치마다 배정된 길이를 가지는 벡터가 없습니다) 다른 방식으로 정보를 얻어야 합니다. 아래 그림을 보면, 점전하를 기준으로 방사형으로 뻗어 나갈수록 선의 밀도가 점점 줄어드는 모습을 볼 수 있는데, 선의 밀도가 클수록 전기장의 세기가 크고, 선의 밀도가 작을수록 전기장의 크기는 작다고 해석할 수 있습니다.

이번엔 전하가 두 개 있는 상황을 생각해봅시다. 아래 그림과 같이 두 전하가 서로 극성이 같거나 다른 경우로 나뉘는데, 두 경우 모두 선의 모양은 다를지언정 어느 위치에서 선은 서로 교차하지 않아야만 합니다. 만약 어느 위치에서 선이 교차한다면 그 지점에서의 전기장 방향이 두 갈래로 갈라진다는 뜻이므로 전혀 말이 안 됩니다.
또한 두 전하의 극성이 같은 경우에 가운데는 전기장이 서로 상쇄되어 $\mathbf{0}$이 되는데, 아래 그림에서 가운데 지점에 그어진 선이 없어 밀도가 0이 되므로, 이는 선의 밀도를 전기장의 세기로 해석하는 방법의 결과와 일치합니다.


위와 같이 선을 이용해 전기장을 이해하는 방법은 기존에 어떤 한 점에서 벡터 정보를 바로 주는 벡터장에서는 느낄 수 없었던 전하로부터 전기장이 '뻗어나간다 혹은 빨려 들어간다'는 느낌을 주게 됩니다.
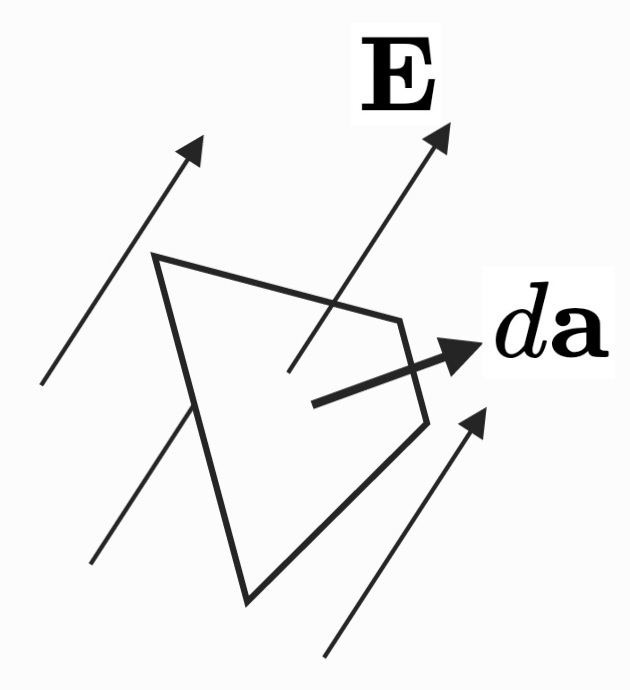
한 가지 짚고 넘어가야 할 점은, 전하로부터 그려지는 전기장선의 개수는 사실 그리는 사람의 마음이라서, 개념적으로만 위 해석을 받아들이는 게 좋습니다. 어찌 됐던, 위와 같은 해석을 받아들인다면 전기 선속의 정의를 좀 더 쉽게 파악할 수 있습니다. 어떤 면적 $S$를 통과하는 '전기 선속(Electric Flux)' $\Phi_E$의 정의는 다음과 같습니다. $$ \int_S \mathbf{E} \cdot d\mathbf{a}. $$ 전기력선의 개념으로 위 식을 이해한다면, 전기 선속은(혹은 간략히 'Flux'라고 부르기도 합니다) 면적 $S$를 통과하는 선의 개수를 의미합니다. 앞서 말했듯이 사실 선의 개수는 그리는 사람의 마음이긴 합니다만, $\mathbf{E}$의 세기는 선의 밀도와 비례하고, 결국 $\mathbf{E} \cdot d\mathbf{a}$는 $d\mathbf{a}$를 지나가는 선의 개수와 비례하게 됩니다.
내적의 사용에 대해서도 생각해보겠습니다. 면 $d\mathbf{a}$가 전기력선과 수직하게 위치하면 그 면적을 통과하는 선이 더 많아질 거고, 수평하게 위치하면 통과하는 선이 없어질 겁니다. 따라서, $d\mathbf{a}$의 법선 벡터(normal vector)와 그 면적을 지나가는 $\mathbf{E}$의 방향을 내적하면, 두 벡터가 같은 방향(수평)일 때 최대, 수직일 때 최소(0)값을 표현할 수 있습니다.
다음 시간에는 위 전기 선속을 이용한 가우스 법칙을 공부해보면서 몇 가지 예시로 문제를 풀어보겠습니다.
'Physics > Electrodynamics' 카테고리의 다른 글
| 전기력, 쿨롱의 법칙과 중첩의 원리 (Electric Force and Superposition Principle) (0) | 2022.11.26 |
|---|

댓글