우리는 실생활에서 10진수(Decimal)에 굉장히 익숙합니다. 10진수란 0~9 사이의 문자들을 이용해 수를 기록하는 방법입니다. 하지만 컴퓨터는 2진법(Binary System)을 이용해 수를 표현합니다. 2진법은 0과 1만으로 수를 표현하는 방법을 말하고, 이때 표현된 수를 이진수(Binary number)라고 부릅니다.
컴퓨터에서 0 혹은 1의 값을 가질 수 있는 하나의 칸을 '비트(Bit)'라고 부르며, 1bit는 자료를 저장하는 가장 작은 단위입니다. 오늘은 컴퓨터가 이루고 있는 자료의 형태인 2진수 체계에 대해서 얘기해보겠습니다.
유래
2진법은 16~17세기 유럽에서 여러 학자들에 의해 연구되었는데 특히 라이프니츠(Gottfried Wilhelm Leibniz)에 의해서 정립되었습니다. 라이프니츠는 중국의 '역경(易經)'이라는 유교 경전에서 2진법의 영감을 얻었는데, 이는 역경이 '도교(道敎)'라는 중국의 민족종교의 이중성 즉, 음과 양에 기반을 두고 있기 때문입니다.
이진수 표현
그렇다면 2진법은 수를 어떻게 표현하는지 알아봅시다. 앞으로 어떤 수 $x$를 표현할 때, 10진수 표현은 $x_{10}$, 2진수 표현은 $x_{2}$로 표기하겠습니다.
2진수는 0과 1만으로 수를 표현하기 때문에 0과 1은 쉽게 표현이 가능합니다. 자세히 쓰면 $0_{10} = 0_{2}$, $1_{10} = 1_{2}$와 같습니다. 문제는 2부터 시작인데 10진수는 0~9까지의 문자를 사용할 수 있으므로 $2_{10}$라고 그냥 쓸 수 있지만, 2진수는 자릿수를 하나 올려 $10_{2}$으로 표현됩니다. 수의 크기가 늘어남에 따라 2진수의 자릿수도 계속 늘어납니다. $$ \begin{align} 0_{10} & = 0_{2} \\ 1_{10} & = 1_{2} \\ 2_{10} & = 10_{2} \\ 3_{10} & = 11_{2} \\ 4_{10} & = 11_{2} \\ 5_{10} & = 100_{2} \\ & \vdots \end{align}$$ 혹은 다음과도 같이 표현될 수 있는데, 예로 $$ 423_{10} = 4 \cdot 10^2 + 2 \cdot 10^1 + 3 \cdot 10^0$$와 같이 해당 수를 표현하는 진수(10)에 각 자릿수의 위치(3, 2, 1의 자리)를 거듭제곱한 후, 각 자릿수에 있는 수(4, 2, 3)를 곱하고 모두 더하면 기존의 수와 같음을 알 수 있습니다. 이는 2진수에서도 마찬가지인데, $423_{10} = 110100111_{2}$이고, 아래와 같이 표현할 수 있습니다. $$ \begin{align} 423_{10} = & 110100111_{2} \\ = & 1 \cdot 2^8 + 1 \cdot 2^7 + 0 \cdot 2^6 + 1 \cdot 2^5 + 0 \cdot 2^4 \\ & + 0 \cdot 2^3 + 1 \cdot 2^2 + 1 \cdot 2^1 + 1 \cdot 2^0 . \end{align}$$ 2진수로 표현된 수의 각 자릿수는 10의 자리가 아니라, $2^y$자릿수로 표현이 가능합니다.
이를 통해 우린 2진수를 좀 더 쉽게 구할 수 있는 아이디어를 얻을 수 있는데, 위의 긴 식에서 $2^0$자릿수를 제외하면 모든 항이 2로 나눌 수 있고, $$ \begin{align} 422_{10} + 1_{10} = & (1 \cdot 2^8 + 1 \cdot 2^7 + 0 \cdot 2^6 + 1 \cdot 2^5 \\ & + 0 \cdot 2^3 + 1 \cdot 2^2 + 1 \cdot 2^1) + (1 \cdot 2^0) \end{align} $$ $2^0$자릿수를 제외하고 다시 2로 나누면 기존의 $2^1$항이 $2^0$항이 되고, 이때 $2^0$의 계수를 다시 걸러낼 수 있습니다. $$ \begin{align} 422_{10} = & (1 \cdot 2^8 + 1 \cdot 2^7 + 0 \cdot 2^6 + 1 \cdot 2^5 \\ & + 0 \cdot 2^4 + 0 \cdot 2^3 + 1 \cdot 2^2 + 1 \cdot 2^1) \\ \Rightarrow 211_{10} = & 210_{10} + 1_{10} = (1 \cdot 2^7 + 1 \cdot 2^6 + 0 \cdot 2^5 \\ & + 1 \cdot 2^4 + 0 \cdot 2^3 + 0 \cdot 2^2 + 1 \cdot 2^1) + (1 \cdot 2^0). \end {align}$$이때, 반복되어 나오는 $2^0$의 계수는 결국 2로 나누었을 때의 나머지가 되고, 이를 통해 $423_{10} = 110100111_{2}$라는 사실을 아래와 같이 우리가 굉장히 익숙한 방식으로 구할 수 있게 됩니다.

위 내용은 2진법뿐만 아니라, 4, 8, 16진법 등, 다른 수 표현에도 똑같이 적용되며, 16진법 같은 경우 10~15까지 알파벳 A~F로 표현합니다.
이진법의 정수 표현
정수는 음수를 가지고 있기 때문에 이진법으로 어떻게 음수를 표현할 것인지 생각해야 합니다. 가장 생각하기 쉬운 방법은 음의 부호를 나타내는 자리 하나를 더 만드는 겁니다.
어떤 수를 이진수 4자리로 표현한다고 가정해봅시다. 0, 1이 들어가는 하나의 자리를 컴퓨터에서는 비트라고 부르니, 4비트로 수를 표현한다고 말할 수 있습니다. 예를 들어 $$\begin{align} 3_{10} & = 0\,\,011_2 \\ -3_{10} & = 1\,\, 011_2 \end{align}$$와 같이 양수면 맨 앞자리가 0, 음수면 1로 만들 수 있습니다.
하지만 위와 같이 표현하면 문제가 생기는데, 바로 0을 표현하는 방법이 두 가지로 갈라진다는 겁니다. $$ \begin{align} 0_{10} & = 0\,\,000_2 \\ -0_{10} & = 1\,\,000_2. \end{align}$$
또 다른 문제점은 연산이 어려워진다는 겁니다. $3_{10}$과 $-1_{10}$을 더하는 연산을 생각해봅시다. 10진수로는 당연히 $3_{10} + (-1_{10}) = 2_{10}$이지만, 이를 2진수로 표현하여 단순히 같은 자리끼리 더하면 $$ \begin{array}{r} 0 \,\, 011 \\ +1 \,\, 001 \\ \hline 1 \,\, 100 \end{array} $$ 따라서 $1 \,\, 100_2 = -4_{10}$가 되어버립니다. 따라서 위와 같은 방법으로 연산을 하려면, 우리는 제대로 된 값이 나오는 복잡한 연산 코드를 컴퓨터에 따로 넣을 수밖에 없습니다.
2의 보수(2's Complement)
위와 같은 문제를 해결하기 위해 등장한 것이 바로 '2의 보수(2's Complement)'입니다. 2의 보수는 1의 보수(1's Complement)로부터 구할 수 있는데, 어떤 2진수의 1의 보수란, 0이 들어간 자리는 1, 1이 들어간 자리는 0으로 바꾸면 얻을 수 있고, 2의 보수는 1의 보수에서 1을 더해 얻을 수 있습니다. $3_{10} = 0011_{2}$을 예를 들어 2의 보수를 구해봅시다. $$ \begin{align} & 0011 \\ 1\text{'s complement : } & 1100 \text{ (위에서 0과 1을 바꿈)} \\ 2\text{'s complement : } & 1101 \text{ (1의 보수에 1을 더함)} \end{align} $$ 위에서 알 수 있듯이 어떤 이진수 a의 2의 보수는 a와 더해졌을 때, 주어진 비트 수를 한자리 초과하는 $2^n_{10}$이 나오는 수를 말합니다. $$ \begin{array}{r} 0011 \\ + 1101 \\ \hline 1\,0000 \\ = 16_{10} \\ = 2^4_{10} \end{array} $$
오버플로우(Overflow)
이때, 표현 가능한 4비트 자릿수를 넘어가는 일이 발생하는데, 넘어간 1을 버리면 $0000_{2} = 0_{10}$이 됩니다. 따라서 어떤 2진수 a의 2의 보수를 -a로 사용하면, 두 이진수를 더해서 표현 가능한 비트 자릿수를 넘어가는 수는 버리고, 나머지 수로 더해진 두 이진수의 값을 표현할 수 있습니다. 굳이 음수에 대한 연산을 따로 정의하지 않고 말이죠. 아래 예를 통해 계산 결과를 확인해 보겠습니다. $$ \begin{align} & 5_{10}-3_{10} \\ = & 0101_2 + 1101_2 \\ = & 10010_2 \\ = & 0010_2 \quad \text{(맨 앞 1 버림)} \\ = & 2_{10} \end{align} $$ 계산 결과가 바르게 나온 것을 확인할 수 있습니다. 이처럼, 표현 가능한 자리수를 넘어가는 현상을 '오버플로우(Overflow)'라고 부르며, 2의 보수와 오버플로우 현상을 사용하여 음수와의 덧셈을 훨씬 쉽게 수행할 수 있게 됩니다.
보수라는 개념은 사실 2진수의 연산에만 국한되는 얘기는 아니고, 여러 진수에 대해서도 정의하여 사용할 수 있습니다. (참조 : Method of complements)
0의 2의 보수 표현
$0 _{10} = 0000_2$의 2의 보수 표현을 구해보면 아래와 같습니다. $$ \begin{align} & 0000 \\ 1\text{'s complement : } & 1111 \text{ (위에서 0과 1을 바꿈)} \\ 2\text{'s complement : } & 1\,0000 \text{ (1의 보수에 1을 더함)} \\ \text{Overflow 1 버림 : } & 0000. \end{align} $$따라서, 2의 보수 체계와 오버플로우를 이용하면 0에 대한 표현도 $0000_2$로 유일 해지며, 0 표현에 대한 모호함을 없앨 수 있습니다.
2의 보수 체계의 수 표현 범위
2의 보수 체계를 사용한다면 $1000_2$는 $8_{10}$이 아닌 $-8_{10}$로 사용합니다. 납득할만한 이유를 들자면 다음과 같습니다. $0001_2 \sim 0111_2$을 모두 양수인 $1_{10} \sim 7_{10}$으로 해석했을 때, 각 수들의 2의 보수는 $1111_2 \sim 1001_2$, 다시 말하면, $-1_{10} \sim -7_{10}$가 됩니다. 이때 $1000_2 + 0001_2 = 1001_2$는 $-7_{10}$이 되기 때문에 $1000_2 = -8_{10}$로 해석해야 합니다. 안타깝게도 양수 8은 표현이 안됩니다. 근본적인 원인은 4비트 표현에서 각 비트마다 표현할 수 있는 수가 0과 1, 두 가지가 있으므로 총 $2^4 = 16$개의 수 표현이 가능하기 때문입니다. 0은 2의 보수 표현에서 $0000_2$ 하나의 표현만을 가지므로 나머지 표현 가능한 수는 15개가 되고, -8, -7,... -1, 1,... 7, 8 총 16개의 숫자가 나머지 자리를 하나씩 차지하면 자리를 차지하지 못하는 수가 하나 생기게 됩니다. 그것이 가장 큰 수인 8이 되는 것이죠. 이때, 가장 작은 수 $-8_{10} = 1000_2$의 2의 보수는 $1000_2 \rightarrow 0111_2 \text{ (1의 보수)} \rightarrow 1000_2 \text{ (2의 보수)}$로 자기 스스로와 같은 수가 되는 특이한 현상이 일어납니다. 이렇게, 주어진 비트 자릿수에서 가장 작은 수를 'Most negative number'라고 부릅니다. 아래는 4비트로 표현된 수들을 나타낸 표입니다.
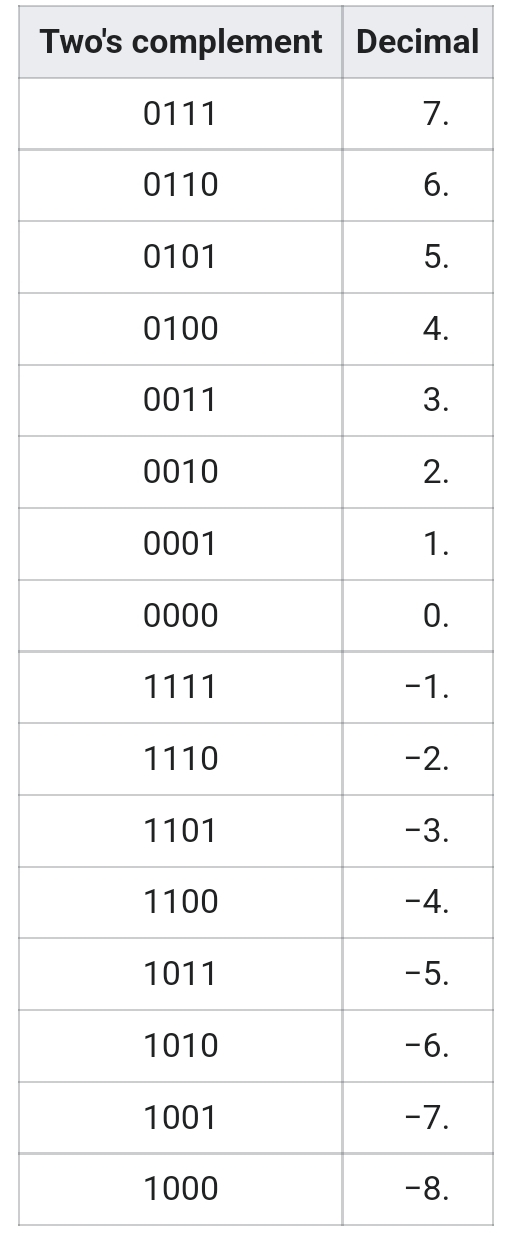
Most negative number 같은 특이한 수 때문에 재밌는 현상이 일어나기도 하는데, 예를 들면 컴퓨터 코드를 작성할 때, abs(absolute value, 절댓값)값이 원하는 값을 주지 않는 경우가 생기기도 합니다. 관심 있는 분들은 이곳에 방문하여 글을 한 번 읽어보시길 바랍니다.
댓글